Here we attempt a simple explanation of the blockchain for a not overly technical audience.
Download the Essence of the Blockchain PDF
1 Introduction
The blockchain is a testament to the power of a single cryptographic primitive – the hash function. Really nothing else is required, so if you can get your head around the hash function, you can understand the basics of the blockchain.
2 The Hash Function
A cryptographic hash function takes one input and calculates one output. For example for the input “We hold these truths to be self-evident”, the well known hash function SHA256 produces the output
84ba74b2661c87470665a1a5f5ab526afcf266f8c5effb795bef2d2514a8afd3
For the slightly different input “we hold these truths to be self-evident” (note the lower case w), the output is
246160c031a4ddd9d940e931721fdec7e72087c8eccf5ea5621bb15d22959c19
That tells us a few things about a hash function. The output bears no obvious relationship to the input, indeed it looks completely random. A tiny change to the input produces a completely different output. You will need to take my word for it that given just the output its impossible to determine the input. For this reason the hash function is often called a “one way” hash function. Also its impossible to find two different inputs which give the same output. For the function SHA256, the 256 refers to the fact that the output is always the same length (actually 256 bits), independent of the length of the input.
And that’s it for the cryptography!
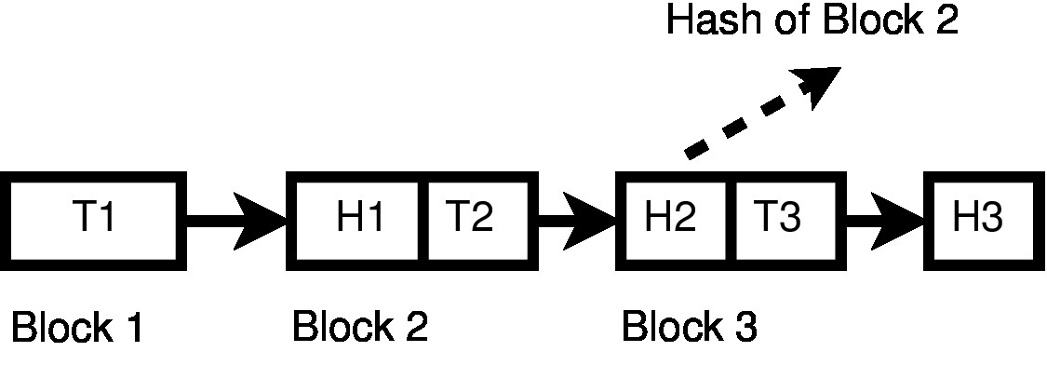
Fig. 1. A simple hash chain
3 A basic hash chain
A basic hash chain looks something like figure 1.
Here the T are “transactions” of some sort. Examine this diagram for a while, and appreciate the power of the chaining. The value H3 is calculated by hashing the whole of block 3, which includes the hash of block 2, which in turn includes the hash of block 1 etc. Note that because of the one-wayness of the hash function, this chain can only be calculated from left-to-right. So already we have some of the properties we want. This hash chain can potentially be used as an immutable record of transactions. Any attempt to tamper with it can be detected, as the hashes will change.
4 The blockchain
However there is a huge problem. Anyone can simply change an internal transaction, and recalculate the rest of the chain, and claim that this is now the valid hash chain. To prevent this let us make extending the chain a costly process. The idea is that anyone trying to change a transaction embedded deep within the hash chain, will find it very hard to compute an alternate chain from that point on which will catch-up with and overtake the one true chain.
This is the blockchain.
To achieve this we insist that the hash values must be numerically smaller than a certain limit. Now this isn’t going to happen naturally so we need to help it along a little.
Taking our previous example, the idea now is to find a hash of “We hold these truths to be self-evident XXXX”, where we get to search for a 4-digit number XXXX in the range 0000 to 9999, which will generate a hash less than the current limit, which for demonstration purposes we will assume is
006d6a61d20638b8e5c026930c3e6039a33ce45964ff2167f6ecedd419db06c1
Note that this number already starts with 00, so its already relatively small.
The value of XXXX is called a “nonce”. We don’t really care what it is as long as it does the job. Since the hash value is essentially random, there is no better way to find a good nonce than to try every number in the range 0000 to 9999 one after the other, until the hash value becomes less than the current limit. In this case we find that the nonce 0317 does the trick. The hash value using this nonce is clearly less than the above limit.
001fafa1003be48899c0684ea3f5b060e5661d588d5d1c8fd34014244e1b099b
However it took 317 evaluations of the hash function to find it. Yes, you guessed it, this is the well known mining process made famous by Bitcoin. Only by offering such a proof-of-work can a miner ensure that the block they are working on is the next one to get added to the end of the blockchain. But how to incentivise mining? With Bitcoin this is neatly solved in the best possible way by financially rewarding the miners – in Bitcoin of course. This prize goes to the first miner who can present a proof-of-work for a valid block, that is with a hash value less than the current limit for a new block which the majority of other miners accept as being consistent with the rules that govern transactions for a particular application.
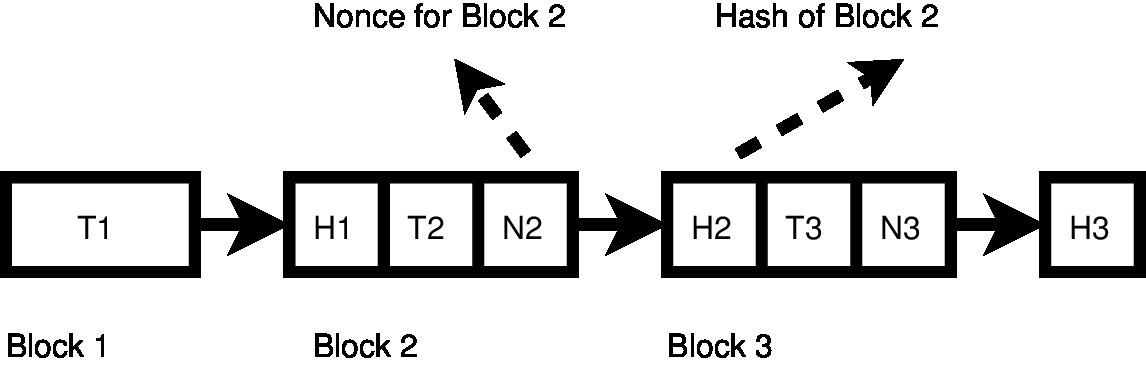
**Fig. 2. **A short blockchain, with nonces
Once a good block has been added, the other miners should accept it, give up their own effort, and start work on the following block. As long as the majority of mining power lies in the hands of the good-guys, all will be well.
Naturally enough the reward system has led to a bit of an arms race between miners, and so the hash limit is continually being adjusted downwards, as its important that the amount of work remains significant even as the mining hardware gets faster.
What if two transactions were offered for inclusion as the next block at the same time? If both blocks are valid the miners will randomly choose between them, but the majority effort will prevail and only one of them will survive. The longest chain is always the true chain.
An attacker might try and jump in and “fork” the chain to their advantage. In a Bitcoin context for example this might represent an attempt at double-spending of some Bitcoin they own. However this requires subverting a majority of the miners, and it is assumed that the majority of the miners will obey the rules regarding the (application dependent) consistency of transactions. This also means that to ensure its own integrity, the blockchain must keep growing, otherwise the time is available for a less well equipped attacker to grow the chain to its own advantage. As long as the honest miners keep mining, and as long as they control a majority of the mining capacity, we will be OK.
In reality of course the miners do a lot more work. An example of an actual hash from the blockchain would be
00000000000000001e8d6829a8a21adc5d38d0a473b144b6765798e61f98bd1d
To find a hash this small is equivalent to tossing a coin until you succeeded in getting a run of 64 consecutive “heads”. That’s a lot of work!
5 Discussion
And that’s basically it - just replace the text “We hold these truths to be self-evident” with the digital representation of a transaction, having designed your own transactional syntax. Of course there is a lot more detail when the idea is applied to a particular context, but we have described the essential ingenious trick behind the blockchain. After that its just a question of what the transac-tions represent, and how they interact. It can be assumed that transactions are related to one another in some way, and that the outcome of old transactions may be superceded by later ones.
An important point - what we have described as individual transactions will probably consist in fact of a large batch of transactions all included inside of a single block. And it is only the hash of all of these transactions that is included in the blockchain hash. The hashing of all the transactions in a block uses an efficient data structure called a Merkle tree. So we have hashes inside of hashes… But we are already getting in way too deep for this simple introduction.
Also its not quite so simple to get this idea to work as we have made it sound. There are a lot of parameters that need to be finely tuned to get a blockchain to work optimally. And while Bitcoin appears to have been incredibly lucky with its initial choices, newer blockchain-based technologies can learn from our experience of Bitcoin and do even better.
You may have heard that elliptic curve cryptography is also required by the blockchain. Well actually thats more of a Bitcoin thing, where elliptic curve crypto is used to digitally sign and verify transactions in and out of individual Bitcoin \wallets", that are external to the blockchain. However it is perfectly possible to deploy a digital signature scheme that only uses hash functions. So there is no intrinsic requirement for elliptic curve cryptography. All you need is a good hash function!



