There are a variety of ways of applying the Karatsuba idea to multi-digit multiplication. These apply particularly well in the context where digits do not use the full word-length of the computer, so that partial products can be safely accumulated without fear of overflow. Here we re-visit the “arbitrary degree” version of Karatsuba and show that the cost of this little-known variant has been over-estimated in the past. We also attempt to definitively answer the question as to the cross-over point where Karatsuba performs better than the classic method.
Download PDF And learn about the Karatsuba variations
1 Introduction
As is well known the Karatsuba idea for calculating the product of two polynomials
can be used recursively to significantly reduce the number of partial products required
in a long multiplication calculation, at the cost of increasing the number of additions.
A one-level application can save 1/4 of the partial products, and a two-level
application can save 7/16ths etc. However application of Karatsuba in this way
is quite awkward, it attracts a large overhead of extra additions, and the
ideal recursion is only available if the number of digits is an exact power of
two.
One way to make Karatsuba more competitive is to use a number base radix that
is somewhat less than the full register size, so that additions can be accumulated
without overflow, and without requiring immediate carry propagation. Here we refer
to this as a “reduced-radix” representation.
Multi-precision numbers are represented as an array of computer words, or “limbs”,
each limb representing a digit of the number. Each computer word is typically the
same size as the processor’s registers, that are manipulated by its instruction set.
Using a full computer word for each digit, or a “packed-radix” representation [7],
intuitively seems to be optimal, and was the method originally adopted by
most multi-precision libraries. However to be efficient this virtually mandates
an assembly language implementation to handle the flags that catch the
overflows that can arise, for example, from the simple act of adding two
digits.
The idea of using a reduced-radix representation of multi-precision numbers
(independent of its suitability for Karatsuba) has long been championed by Bernstein
and his co-workers. See for example [2] for a discussion of the relative merits of
packed-radix and reduced-radix representation. This approach is supported by the
recent experience of Hamburg in his implementation of the Goldilocks elliptic curve
[7]. A reduced-radix representation is sometimes considered to be more efficient [7] –
and this is despite the fact that in many cases it will require an increased number of
limbs.
In [1] is described an elliptic curve implementation that uses this technique to
demonstrate the superiority of using the Karatsuba idea in a context where each
curve coordinate is represented in just 16 32-bit limbs. In fact there is much confusion
in the literature as to the break-even point where Karatsuba becomes superior.
One confounding factor is that whereas Karatsuba trades multiplications for
additions, in modern processors multiplications may be almost as fast as
additions.
Elliptic curve sizes have traditionally been chosen to be multiples
of 128-bits, to provide a nice match to standard levels of security. On the
face of it, this is fortuitous, as for example a 256-bit curve might have its
and
coordinates fit snugly inside of 4 64-bit or 8 32-bit computer words using a
packed-radix representation. Again, as these are exact powers of 2, they might be
thought of as being particularly suitable for the application of the Karatsuba idea.
However somewhat counter-intuitively this is not the case – if Karatsuba is to be
competitive the actual number base must be a few bits less than the word size in
order to facilitate addition of elements without carry processing (and to support the
ability to distinguish positive and negative numbers). So in fact a competitive
implementation would typically require 5 64-bit or 9 32-bit words, where 5
and 9 are not ideal polynomial degrees for the application of traditional
Karatsuba.
What is less well known is that there is an easy to use “arbitrary degree” variant of
Karatsuba (ADK), as it is called by Weimerskirch and Paar [12], which can save
nearly 1/2 of the partial products and where the polynomial degree is of no concern
to the implementor. In fact this idea has an interesting history. An earlier draft of the
Weimerskirch and Paar paper from 2003 is referenced in [10]. But it appears to have
been discovered even earlier by Khachatrian et al. [8], and independently by David
Harvey, as reported in Exercise 1.4 in the textbook [3]. Essentially the same idea was
used by Granger and Scott [4], building on earlier work from Granger and Moss
[5] and Nogami et al. [11], in the context of a particular form of modular
arithmetic.
Here we consider the application of this variant to the problem of long integer
multiplication. Since the number of partial products required is the same as the well
known squaring algorithm, squaring is not improved, and so is not considered further
here. We restrict our attention to the multiplication of two equal sized numbers, as
arises when implementing modular arithmetic as required by common cryptographic
implementations.
2 The ADK algorithm
This algorithm is described in mathematical terms in [3], [8] and [12]. However here
we have used the subtractive variant of Karatsuba to some advantage to get a simpler
formula, as pointed out to us by [13].
| (1) |
Observe that in additive form the formula is more complex:-
| (2) |
This clearly involves more additions and subtractions than equation (1). In fact we
find the mathematical description unhelpful in that it makes the method look more
complex than it is. It also makes it difficult to determine its exact complexity. To that
end an algorithmic description is more helpful.
Algorithm 1: The ADK algorithm for long multiplication
INPUT: Degree , and radix
INPUT: where
OUTPUT: , where and
1: function ADKMUL()
2: for do
3:
4: end for
5:
6:
7: for do
8:
9:
10: for do
11:
12: end for
13:
14: end for
15: for do
16:
17:
18: for do
19:
20: end for
21: t
22: end for
23: return
24: end function
The number of multiplications and additions required can be confirmed by a simple
counting exercise. For clarity we have not included the final carry propagation, which reduces
the product
to a radix
representation. A fully unrolled example of the algorithm in action for the case
is
given in the next section.
3 Comparing Karatsuba variants
As an easy introduction consider the product of two 4 digit numbers,
. The
School-boy method (SB) requires 16 multiplications (muls) and 9 double precision
adds, which is equivalent to 18 single precision adds. In the sequel when comparing
calculation costs a “mul” M is a register-sized signed multiplication resulting in
a double register product. An “add” A is the addition (or subtraction) of
two registers. We also make the reasonable assumption that while add, shift
or masking instructions cost the same on the target processor, an integer
multiply instruction may cost more. So the cost of the SB method here is
16M+18A.
| (3) |
A final “propagation” of carries is also required. Assuming that the
number base is a simple power of 2, this involves a single precision
masking followed by a double precision shift applied to each digit of the
result. The carry must then be added to the next digit. If multiplying two
digit numbers the extra
cost is equivalent to
adds. Here we will neglect this extra contribution, as it applies independent of the
method used for long multiplication.
Using arbitrary-degree Karatsuba (or ADK), the same calculation takes 10 muls
and 11 double precision adds and 12 single precision subs. The total cost is
10M+34A. So overall 6 muls are saved at the cost of 16 adds
| (4) |
Here square brackets indicate values already available from the calculation.
Hopefully the reader can see the pattern in this example in order to easily extrapolate
to higher degree multiplications.
It is an interesting exercise to repeat this calculation using one level of
“regular” Karatsuba, and simplifying the result. As can be seen in equation 5 the
same calculation requires 12 muls, 10 double precision adds and 4 single
precision subs, or equivalently 12M+24A, so 4 muls are saved at the cost of 6
adds.
| (5) |
Observe that only ,
and
are
calculated differently. Using two levels of Karatsuba (equation 6), requires 9M+38A,
so 7 muls are saved at the cost of 20 adds.
| (6) |
Now only
is calculated differently from the ADK approach. It is noteworthy that in [1] the
authors deployed two levels of standard Karatsuba, and apparently did not consider
the ADK method. However since the ADK approach works on a digit-by-digit basis,
and thus applies seemlessly independent of the number of digits, it would appear to
offer a nice easily applied compromise solution that extracts a big part of
the Karatsuba advantage, without causing an explosion in the number of
additions.
In terms of the number of partial products required, its performance is always at
least as good as that obtained by applying one level of regular Karatsuba. This may
represent an easily achieved “sweet spot” of relevance to applications involving
medium sized numbers, as may for example apply in the context of Elliptic Curve
Cryptography.
In passing we observe, as also noted in [3], that the ADK method can be used as
an amusing alternative algorithm for pencil-and-paper long multiplication. We
would not be surprised to learn of its use in the recreational mathematics
literature.
4 Numerical stability
Before proceeding we need to address the problem of numerical stability. We start by
assuming that both numbers to be multiplied are fully normalized, that is each digit of
is in the
range . If
they are not, they can be quickly normalized using a fast mask and shift operation
(which works even if some of the digits are temporarily negative). For numerical stability
of the long multiplication it is important that the sum of double-precision products
that form each row of equation 3, do not cause a signed integer overflow. Assume that
where
on a
-bit
wordlength computer. Then the product of two such numbers could be as big as
. The longest
row consists of
such numbers, plus a carry from the previous row. So each row could not be larger than
. Since it
must be possible to distinguish the sign of each partial product this must be strictly less
than .
For the common wordlengths of
and -bits,
and for numbers of the sizes relevant to elliptic curve cryptography, we would expect
to be
or
on a 32-bit
computer, and
or for
a 64-bit computer. Too large and the stability criteria will not be met. Too small and
too many words will be required to represent our numbers, with a loss of
efficiency.
We would assume that normally the largest radix possible would be
used that is compatible with this stability condition. However there may
be other factors at play which might dictate a slightly smaller choice for
– for
example if reduction were merged with multiplication [4], or if it were regarded as
desirable that field elements could be added without normalization prior to
multiplication [7].
5 The true cost of ADK multiplication
In [12] the number of multiplications and additions required for the
application of the ADK method is calculated, in the context of polynomial
arithmetic. There it is worked out that its performance compared to
the school-boy method, given a multiplication to addition cost ratio of
, is such that they
are equivalent for
irrespective of the degree of the polynomials. The rather neat conclusion might be
that unless multiplication takes more than 3 times as long as an addition, the method
brings no advantage. And for many real-world processors with hardware support for
integer multiplication, this may not be the case.
However here we are interested in multi-precision arithmetic, which is
a little different. While all of the additions in the SB method are double
precision, the subtractions required by the ADK method are only single
precision. Furthermore the cost function used for ADK in [12] appears to be
incorrect. The true cost in terms of single precision additions is actually only
for the ADK method,
compared to the
required by SB. In [12] the number of additions is calculated as being of the order of
. This dramatically
changes the balance between the two contenders. Recall that for SB the number of muls is
, while for the
ADK method it is .
An immediate and striking conclusion is that for
the
total number of muls and adds for ADK becomes less than the total required for
SB.
Interestingly Khachatrian et al. [8] appear to have got it wrong as well,
over-estimating the number of additions required to an even greater extent, as always
requiring 50% more additions than the SB method. However these previous
over-estimates may be explained by the authors considering only a packed-radix
representation.
Processor designers go to great lengths to cut the cost in cycles of a mul instruction,
even getting it down to 1 clock cycle, the same as that required for an add. However a
mul will always require more processor resources, and thus a hidden extra cost will
probably show up in actual working code. For example in a multi-scalar architecture
only one processor pipeline might support hardware multiplication, whereas all
available pipelines will allow simultaneous execution of adds, so whereas one mul can
execute in 1 cycle, two or more adds might execute simultaneously. The actual
break-even point between ADK and SB can only be determined on a case-by-case
basis via an actual implementation. In this next table we calculate the ratio
between the costs of muls and adds that mark the expected break-even between SB
and ADK.
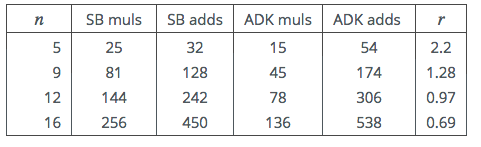
Table 2: Operation Counts
This would appear to settle the matter: A variant of Karatsuba should be used for
all multi-precision multiplications that involve numbers with 12 or more limbs. A
caveat might be that the simplicity of the SB method might favour a compiler in
terms of the number of memory accesses and register move instructions (not
considered here) which it might require. However we suspect that any such advantage
would be outweighed by the hidden resource consumption of even the fastest integer
multiply.
On the other hand it remains a real possibility that a packed-radix implementation of
the School-Boy method written in carefully hand-crafted assembly language
might prove superior on particular processors, even beyond the 12 limb limit
(bearing in mind that a packed-radix representation may actually require less
limbs). This could only be established experimentally. A useful resource for
comparison purposes would be the well known GMP multi-precision library
[6].
6 Some results
We tested our results on an industry standard Intel i3-4025U 1.9GHz 64-bit
processor running in Windows. This is a simple head-to-head comparison of the
reduced-radix SB and ADK methods. The test code was written in C, and
compiled using the GCC compiler (version 5.1.0) with maximum optimization.
It includes the carry propagation code. The multiplication code was fully
unrolled, as a compiler cannot always be trusted to do this automatically.
Our experience would be that optimized compiler output like this for Intel
processors is very hard to improve upon, even using hand-crafted assembly
language.
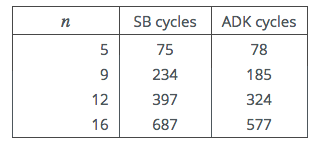
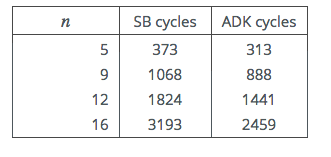
Table 3: Intel i3-4025U Cycle Counts
These results more than support the conclusion to be drawn from table 2: In fact
on this processor the cross-over point occurs already with just 9 limbs. On examining
the generated code, it was observed that the number of mul and add-equivalent
instructions were as predicted in the analysis above. However an inspection of the
generated code also confirmed our suspicion that the ADK code generated more
register-register move instructions and memory accesses. On some processors this
could offset the ADK advantage.
7 Conclusion
In this note we have dusted off an old oft-rediscovered trick that we would suggest has
not received sufficient attention from those interested in efficient cryptographic
implementations. We have demonstrated that it is much more efficient than
previously thought. We have established a concrete break-even point where Karatsuba
variants should be considered ahead of the classic school-boy method for long
multiplication.
An obvious extension of the idea applies to Montgomery’s method for modular
reduction without division [9] – details are given in an appendix.
Of course we are not claiming that the ADK method is necessarily the
best choice in all circumstances. A classic recursive Karatsuba may well be
superior in particular cases. For example Hamburg [7] uses a modulus that
chimes particularly well with 1-level of classic Karatsuba. And Bernstein et
al. [1] may well be correct in applying 2-level Karatsuba in their particular
context.
The fact that a multiplication now requires the calculation of the same number of
partial products as a squaring, might encourage implementors to use this
multiplication algorithm for both squaring and multiplication, so that multiplications
and squarings cannot be easily distinguished by some simple kinds of side-channel
attack, like for example a timing attack.
8 Acknowledgements
The author would like to thank Rob Granger, Billy Bob Brumley and Paul
Zimmermann for helpful comments on an earlier draft of this paper.
References
1. Daniel J. Bernstein, Chitchanok Chuengsatiansup, and Tanja Lange.
Curve41417: Karatsuba revisited. Cryptology ePrint Archive, Report 2014/526,
2014. http://eprint.iacr.org/2014/526.
2. Daniel J. Bernstein, Niels Duif, Tanja Lange, Peter Schwabe, and Bo-Yin Yang.
High-speed high-security signatures. Cryptology ePrint Archive, Report 2011/368,
2011. http://eprint.iacr.org/2011/368.
3. R. Brent and P. Zimmermann. Modern Computer Arithmetic. Cambridge
University Press, 2010.
4. R. Granger and M. Scott. Faster ECC over
.
In Public-Key Cryptography – PKC 2015, volume 9020 of Lecture Notes in
Computer Science, pages 539–553. Springer Berlin Heidelberg, 2015.
5. Robert Granger and Andrew Moss. Generalised Mersenne numbers revisited.
Mathematics of Computation, 82:2389–2420, 2013.
http://arxiv.org/abs/1108.3054.
6. Torbj�rn Granlund and the GMP development team. GNU MP: The GNU
Multiple Precision Arithmetic Library, 6.1.0 edition, 2015. http://gmplib.org/.
7. Mike Hamburg. Ed448-Goldilocks, a new elliptic curve. Cryptology ePrint
Archive, Report 2015/625, 2015. http://eprint.iacr.org/2015/625.
8. G. Khachatrian, M. Kuregian, K. Ispiryan, and J. Massey. Faster
multiplication of integers for public-key applications. In Selected Areas in
Cryptography, volume 2259 of Lecture Notes in Computer Science, pages 245–254.
Springer Berlin Heidelberg, 2001.
9. P. Montgomery. Modular multiplication without trial division. Mathematics
of Computation, 44(170):519–521, 1985.
10. P. Montgomery. Five, six and seven term karatsuba-like formulae. IEEE
Transactions on Computers, 54(3):362–369, 2005.
11. Y. Nogami, A. Saito, and Y. Morikawa. Finite extension field with modulus
of all-one polynomial and representation of its elements for fast arithmetic
operations. IEICE Transactions on Fundementals of Electronics, Communications
and Computer Sciences, E86-A(9):2376–2387, 2003.
12. Andre Weimerskirch and Christof Paar. Generalization of the Karatsuba
algorithm for efficient implementations. Cryptology ePrint Archive, Report
2006/224, 2006. http://eprint.iacr.org/2006/224.
13. P. Zimmermann. Personal communication, January 2015.
More results
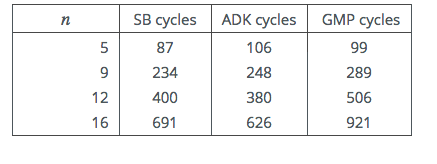
We carried out further tests on a variety of platforms. In all cases we used the GCC
compiler tools. Where the well known GMP library could be installed, we provide a
comparison with its assembly language mpn_mul_basecase() packed-radix SB
implementation. However it should be noted that whereas the GMP code is only
partially unrolled, ours is fully unrolled.
First up is a rather old Intel Core i5 chip running under the Ubuntu OS, and using
GCC version 5.2.1.
Table 4: 64-bit Intel i5-M520 Cycle Counts
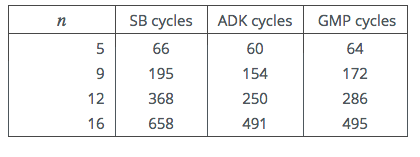
Next a more modern i5 variant, running on an Apple Mac Mini.
Table 5: 64-bit Intel i5-4278U Cycle Counts
Finally results for an old 32-bit Intel Atom processor, using GCC version
4.8.4
Table 6: 32-bit Intel Atom N270 Cycle Counts
Example Code
Here we present an example of the loop unrolled C code for the SB and ADK
methods that we used in our tests. In this small example the number of limbs
in
and
is 5. Code for carry propagation is included. In practise this code is
automatically generated by a small utility program for any value of
.
typedef int64_t small;
typedef __int128 large;
#define B 61 // bits in radix
#define M (((small)1<<B)-1) //Mask
void sbmul5(small *x,small *y,small *z)
{
large t,c;
t=(large)x[0]*y[0]; z[0]=(small)t&M; c=t>>B;
t=c+(large)x[1]*y[0]+(large)x[0]*y[1]; z[1]=(small)t&M; c=t>>B;
t=c+(large)x[2]*y[0]+(large)x[1]*y[1]+(large)x[0]*y[2]; z[2]=(small)t&M; c=t>>B;
t=c+(large)x[3]*y[0]+(large)x[2]*y[1]+(large)x[1]*y[2]+(large)x[0]*y[3];